|
To his credit, he gets off to a great start, building support for
one of the key foundations of Einstein's theories. He describes
the motions of the Earth and the sun amongst the galaxies and the universe
at large, using this to demonstrate our inability to find an absolute frame
of reference against which things might be measured. Excellent.
Sagan: "A million years from now,
Leo might be renamed the constellation of the... radiotelescope,
although I suspect that radiotelescopes then will be as obsolete
as stone spears are now." I'd agree with Sagan there;
I think radiotelescopes won't even last for half that time,
but let's remember this quote when
episode 12 rolls around....
A critical point is reached when Sagan simulates a near-collision between his
fast moving bicycle and a slow moving horse-drawn cart, to demonstrate that
the speed of a "source" of light does not add its own velocity to the speed of light itself.
This example requires some imagination and faith for the result, but okay,
we'll buy that. The question he fails to ask is what effect the velocity
of the observer may or may not have to the speed of light - this is glossed
over as if it doesn't matter.
Einstein's Special Relativity was an attempt to integrate two separate pre-existing
ideas in science which seemed to contradict each other. As of this point,
Sagan has given us hints of both:
From the mechanics of Newton and Galileo comes the Principle of Relativity,
which allows for no absolute frame of reference, only multiple relative frames of reference.
From the world of electrodynamics and optics comes the notion of
light refusing to alter its velocity in accordance with the velocity of its source,
as classical momentum would predict.
That said, the Newton-Galileo principle of relativity
is thrown out the window during a ridiculous sequence
of funny things that supposedly happen "close to the speed of light". Sagan totally
forgets to examine (much less tell the audience) against what kind of "stationary"
frame of reference this almost-speed-of-light is being measured. Without realizing it,
by leaving out such an examination during this sequence,
he ends up IMPLYING that there is a preferred
absolute frame of reference, with a speed limit on top. And he's really creepy about it,
by being authoritative and controlling, instead of inquiring and informative.
This is where the episode then crashes and burns - the rest of the Einstein segments
are SO badly written, that I doubt Sagan or his co-writers understood Einstein's
theories at all. What we end up with is a recycling of a lot of common clichés
and popular misconceptions for content, presented in a style that abandons logic
and religiously embraces a doctrine of rules instead. The amount of false information
Sagan flogs his audience with here makes my skin crawl.
Sagan says: "If the world is to be understood,
if we are to avoid logical paradoxes
when traveling at high speeds
then there are certain rules which must be obeyed.
Einstein called these rules
the Special Theory of Relativity."
What the hell does that first sentence of his really mean?
Einstein gets to write the rules,
which then the universe has to obey,
so as not to challenge our Human minds with a paradox?
Man, that sounds so messed up.
How has this boiled down to OBEYING rules?
This is a common bit of trouble that many professional scientists sink into when
they express the constancy of the speed of light "through the back door",
meaning relative to its source, where it seems to violate Newton's laws of momentum
and cause a cascading re-think of many of the most basic equations in physics.
But to take an important step towards the meaning instead of the math,
it seems helpful to instead express the constancy of the speed of light
"through the front door", meaning relative to its observer.
This is the fascinating bit. According to one of the two principles
Einstein used to construct Special Relativity, electromagnetic radiation (including light)
always seems to be traveling exactly at 299792 kilometers per second
RELATIVE TO THE OBSERVER, no matter how fast the observer thinks he is moving himself.
The observer is the anchoring point for all the wonkiness in Relativity.
How could you possibly know if you were "traveling close to the speed of light",
when you are your own observer, and you still see light traveling at 299792 km/s
relative to yourself? Many thought-experiments on this subject postulate two observers,
moving at different speeds relative to each other. Einstein traditionally stuck
one in a train car and another on the embankment for examples of Special Relativity.
Others have cleverly put both in magic floating labs in space, an example which has the
additional advantage that neither one of them can be sure who is moving and who is at rest,
treating both equally - as the Galilean principle of Relativity would insist.
It's also a bit presumptuous of Sagan and company to imply that Special Relativity
is somehow an expression of fairness in treating all things equal in all frames of reference.
This is precisely because it treats the speed of light, and all forms of electromagnetic
radiation using that speed, differently from everyday large objects moving at everyday speeds.
Einstein always gives light "preferred seating" in all spacetime continuums.
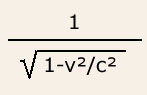
|
|
It is out of this preference that we get different projections of time and space,
which gives us the geometry to calculate the Lorentz factor
( 1 / square root of ( 1 - velocity squared / speed of light squared) ),
a piece of math that will implode whenever we plug in a "velocity" equal to
or greater than the "speed of light". What does this implosion mean?
Does it mean such velocities are impossible to attain?
Or does it mean that the observer will not be able
to properly see the object traveling faster than light relative to himself?
Or is the math merely messed up? How often do any of us really put this
to the test, to see if real world numbers actually fit this formula
better than they fit Newton's?
|
The most memorable example in the episode is probably that of the "Twin Paradox",
which in this variation uses a light-speed motor-scooter instead of the more common
interstellar rocket ship. Trying to use the aging of the twins to demonstrate the
time-dilation effect of Special Relativity presents a big problem. The early 1905
version of Relativity was "Special" because Einstein could only make it work when
the two frames of reference in question moved at a constant velocity relative to
each other, in a perfectly straight line.... which leaves us with no way to
put the two twins side by side again after the experiment is over so that their ages
can be compared. Special Relativity cannot handle acceleration (including changes of direction),
and therefore cannot handle ANY FORCES which would of course cause accelerations.
Gravity is often cited as being beyond Special Relativity; that particular force
is but the tip of a much larger iceberg.
Sagan REALLY puts his foot directly in his mouth
when saying that Special Relativity dictates the result of one twin aging decades
while the other practically doesn't age at all. Note that this result also
heavily implies a preferred frame of reference, where we assume we know who was
really at rest and who was really moving. In fact, if we adhere strictly to all of the
limitations of Special Relativity, the entire "result" can easily be nothing more
than an optical illusion seen "at a distance" by the brother who believes he's sitting at home.
We say it's an optical illusion in part because the brother who believes he's traveling
will also see himself age a lot while the image of his brother at home remains young,
if indeed there is no preferred frame of reference, no gravitational fields,
no accelerations, and no way to get the brothers to re-unite for comparison.
There's really no logical, non-paradoxical way for them to each age while the other does not,
BUT it's easy to see how they might both be seeing similar false images of each other.
IF we stick to Special Relativity alone.
Reciprocating Time-Dilation
In fact, this very bizarre phenomenon, when examined very strictly within the
rules of Special Relativity, seems poised to pull down the entire theory.
I don't yet know how scientists have convinced themselves that it can withstand this.
Four important observations need to be made during the Twin Paradox, as each twin should
examine both his own clock, and his Twin's clock. Unequal aging seems to be a logical
conclusion when only three of the four observations are considered: The "home" twin
sees his own clock advancing normally, but sees that his "traveling" twin's clock
is advancing very slowly. It seems to him that his twin is hardly aging at all.
Meanwhile, the "traveling" twin examines his own clock, and it seems to be advancing normally.
He thinks time is proceeding just fine.
...And many people reciting this idea will cease observing there, and conclude that
time is running slower in the traveler's frame of reference.
But wait, let's bring in the last of the four observations, and obey Galileo's principle of
Relativity while we're at it. Special Relativity allows us no way of making the traveler's
frame of reference any less capable of claiming to be at rest than his brother's frame
of reference. For the traveler, the speed of light appears to be anchored to his eyeball,
not his brother's on Earth. He looks and thinks it's the "home" twin who has a slow clock,
the "home" twin who will remain youthful while he, the traveler, turns old.
How can they both be right? How can reciprocal observations contradict each other?
This may be the greatest Ego joke in physics.
Picture five observers, each gliding
along on a straight line at constant velocity relative to each other. Every single
one of them observes himself as having the fastest clock in the west, while the
others' clocks are all running slow to a larger or smaller degree. Also,
every single one of them observes himself to have the longest measuring rod in town;
everyone else's "rod" has suffered length contraction. Special Relativity,
strictly followed, insists on this result. Can it ever allow any observer
to see a longer rod or a faster clock in someone else's frame of reference? Can it ever
allow a complete set of observations from one frame of reference to actually corroborate
and co-exist with a complete set of observations from any other? A side note:
If the theory accurately describes an optical illusion, it doesn't have to
corroborate. But if it wants to describe reality, perhaps it should.
In this light, other considerations become moot. A return journey for either twin,
in the opposite direction, changes nothing. Negative vectors in the velocity turn
positive when squared (while positive vectors remain positive when squared),
so when flying apart or coming together, each still believes he's got a perfect clock
while his brother's runs slow. Laughably, some people try to make a big deal
over which twin switches to a new frame of reference and which twin remains in the same one.
But remember, strict adherence to Special Relativity does not give you any way to let
that enter your math, or for you to really know. For all it matters, the traveling
twin may be at rest relative to his one frame of reference, while the twin at home
switches to a new one, and takes the Earth, the Solar system, and all other matter
with him into that new frame of reference. All that extra weight means nothing
to a theory that can't consider accelerations, forces, gravity, or mass. Any
turnaround itself is an act of magic in the world of the Theory of Special Relativity,
where nothing counts except uniform motion in a straight line. Both frames
of reference in the separating pair and both in the reuniting pair still all count
as perfectly equal.
Some have said that Einstein himself validated the Twin Paradox at the end of section
four of his original 1905 paper. Two things must be remembered here. Einstein always
wanted a theory of everything, and the difference between Special Relativity and
General Relativity didn't become official until he gave us the 2nd theory in 1916,
additionally formalizing and detailing the difference in his 1920 book. Note that,
in 1905, he does not title his article "Special Relativity" (in German or any other language),
and indeed does not actually confine his thoughts to Special Relativity at all.
He merely knows, with some disappointment, that he hasn't actually got the whole thing
yet as he wants. He knows he hasn't yet nailed accelerations, or curves. That last
paragraph in section four begins "Nimmt man an, dass..." or "One assumes that..."
after which he proceeds to speculate on what General Relativity may find, once he has
it figured out.
Secondly, it may be easy to overlook something important here, in part because section four
begins with Einstein very carefully laying out two frames of reference, in which what
appears to be a perfect sphere from one would appear to be a squashed ellipsoid from the other
due to good ol' length contraction. But, just as you think he may be trying to nail two
synchronized clocks to the wall in one of those two frames of reference
(at a distance for a future experiment), suddenly his set-up becomes the experiment,
and he starts whipping the second clock around in a segmented arc and back to its starting
place, "not aged". Yeah, old Albert then starts drawing conclusions without having
mentioned the now required third frame of reference in which the "moving" clock would seem
to be at rest (in fact a whole series of extra frames of reference, one for
each of those "arc segments"). During its passage through any one of those segments,
Einstein fails to look back at the control clock from within that new frame of reference
(essentially making the last of the four required observations),
where the "stationary" control clock would seem to be the slower one,
in contradiction to his hasty conclusion.
So, how do we treat Einstein? Has he written gospel, or do we subject his writing to
as much scientific rigour as anyone else's? Note that in the equivalent sections of his
1920 book, in chapter 12, he mentions reciprocal observations of length-contraction
contradicting each other,
but has conveniently left out all comment on reciprocal observations of time-dilation.
Perhaps he had had enough trouble trying to prop it up in debates since 1905...
|
There's practically nothing in this eighth episode of Cosmos that comes from
the later Theory of General Relativity. That contains the calculations we would
need to accelerate a twin, then turn him around, and bring him back for comparison.
And then we could start to bring nested gravitational fields into the bargain,
and ask which twin remained at rest relative to the largest gravitational fields
around, and which constantly altered his velocity relative to those fields.
A fascinating question. Cosmos doesn't go there, or deal very carefully
with what it does tackle. Instead it gets irritatingly bossy with the muddle
that it does present, and this will drag episode 8 to the bottom of the rankings.
Museum Piece
There's a good 35 minutes more to this episode after the Einstein bits.
We move on to reference Leonardo da Vinci and his flying inventions in Italy,
where Sagan talks about the Orion propulsion system banned for its use of nuclear
explosions, and a few other proposed systems of interstellar flight. There's an
interesting poignancy here in the comparison, as our history is littered with examples
of technologies that didn't work and widely adopted truths that later proved
to be a bit absurd. Might we one day look back on much of Einstein's Theories in the same
light as we look back on Ptolemy's geocentric view of the universe? Perhaps this
section of the episode correctly evokes the sense that these early concepts
of the science of interstellar travel will become laughable entries in
some future museum of bizarre antiquities...
Also in this episode, Sagan tackles time travel, quickly going through
the infamous grandfather paradox,
plus its elegant Level 3 alternate universe solution. Improvements in languaging
that solution might include calling the universes branching instead of parallel,
and recognizing these being separated along dimensions of choice, rather than time.
My view of course, is that if you're not talking about what scientists officially call
"time as measured by clocks and calendars", you really should use a whole new term
other than "time" to avoid unnecessary confusion. Sagan isn't particularly
biased towards or against any of the concepts of what may be going on or may be
possible with time travel, and is happy to recount all the different theories he's heard of.
Interestingly, Sagan seems to have access to the exact prop, or a near replica,
as that featured in the 1960's film of H.G. Wells' story "The Time Machine".
Sagan sure does get around.
Alternate Tapestry
One easily forgotten sequence discusses the tapestry of history over
footage of a weaving loom in operation. Here we get a few wise words about
Human nature, and some thoughts about important discoveries being made by
different historical figures who undoubtedly would step up to the plate
if our familiar ones somehow didn't manage it. One of the best parts of the
episode, for sure.
Another good bit concerns the formation of the solar system - a very cool
piece of history that is worth the examination that it gets.
Of course, the lengthy evolution cartoon morphing sequence is back,
making one feel that one is sitting through a bit of a re-run of
episode 2.
Yeah, it's got a more exciting background, the narration is different, and
there are some new bits squeezed in concerning dinosaurs and such, but it feels
a bit like Sagan has run out of content early here.
Finally, in the 1990's update, Sagan talks about the scientific background
behind the liberties he took in his novel "Contact", and acknowledges the source
of his ideas. Cool.
So... is the episode rich enough by being full of so many, many interesting thoughts,
that it can still rank well in the 1980 Cosmos line-up? Hmmm... Even when going through
its better bits, it still seems to be embracing an absolute frame of reference for
the universe, anchoring a light-speed limit to that instead of the observer,
and embracing a concept of time-dilation that only looks at it from that one absolute
frame of reference. And then Sagan gives Einstein CREDIT for showing that interstellar travel
is possible, when in fact Sagan's entire messed-up presentation of Einstein has done more to show
how interstellar travel would be highly impractical. Even the better bits are poisoned by
this mode of thinking.
No, sorry. Though the episode certainly has plenty of neat bits, its core
miscalculation remains widespread. I'm saddened to think how much misinformation
became more deeply embedded and perpetuated in our culture because of this episode,
or how it has influenced and continues to influence the tapestry of our Human history and culture.
Take for example the much more recent episode of "The Universe" entitled
"Light Speed", which appears to trip up exactly where it
pays homage to this episode, and yet was capable of greater clarity and tone,
particularly where it took the information and debate to new levels of depth.
Perhaps when we really figure out how best to articulate Einstein's ideas
to ourselves and to new generations, with respectful inquiry instead of enigmatic doctrine,
we might more clearly see which bits are solid and which most require
the self-correction of the scientific process.
This eighth episode "Journeys in Space and Time" misses that ideal mark
by a fairly wide margin in my opinion, and
it remains my least favourite episode of the original Cosmos run.
|



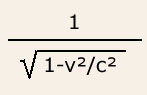


 ("My Mountain" -instrumental intro only)
("My Mountain" -instrumental intro only)







